Question

Find the distance between-8 1/3 and -5 1/2 write your answer as a fraction or mixed number

Answer 1

The given numbers are

`-8(1)/(3),-5(1)/(2)`

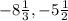
To find the distance between, we must subtract them. However, first, we need to transform each number into a normal fraction

`-8(1)/(3)=(8\cdot3+1)/(3)=-(24+1)/(3)=-(25)/(3)`

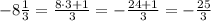
Using the same process, we have

`-5(1)/(2)=-(5\cdot2+1)/(2)=-(10+1)/(2)=-(11)/(2)`

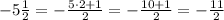
Now, we subtract those fractions

`-(11)/(2)-(-(25)/(3))=-(11)/(2)+(25)/(3)=(-33+50)/(6)=(17)/(6)`

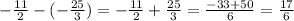
However, we need the result as a mixed number

`(17)/(6)=2(5)/(6)`

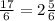
Therefore, the distance is 2 5/6.