Question

Write an equation of the line that is perpendicular to 3x + y = 7 and passes through the point (6,4).

Answer 1

`\begin{gathered} \text{The equation of the line is;} \\ \\ 3y\text{ = x + 6} \end{gathered}`

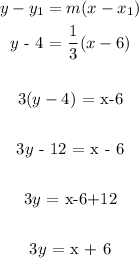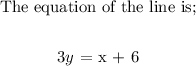
Firstly, we proceed to write the given equation in the standard form of the slope-intercept

That is written as;

`y\text{ = mx + b}`

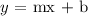
where m represents the slope and b represents the y-intercept

In this case, we can write the given equation as;

`y\text{ = -3x + 7}`

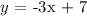
From above, we can see the slope as -3 and the y-intercept as 7

If two lines are perpendicular to each other, then the product of the slopes of the two lines is equal to -1

Let us call the given line, line 1 and the other line, line 2

Thus, we have;

`\begin{gathered} m_1\text{ }* m_2\text{ = -1} \\ \\ -3\text{ }* m_2\text{ = -1} \\ \\ m_2\text{ = }(-1)/(-3)\text{ = }(1)/(3) \end{gathered}`

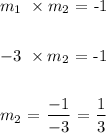
So now, we want to write the equation of a line with slope of 1/3 with the line passing through the point (6,4)

We can use the one-point slope form for this

This can be written as;

`\begin{gathered} y-y_1=m(x-x_1) \\ y\text{ - 4 = }(1)/(3)(x-6) \\ \\ 3(y-4)\text{ = x-6} \\ \\ 3y\text{ - 12 = x - 6} \\ \\ 3y\text{ = x-6+12} \\ \\ 3y\text{ = x + 6} \end{gathered}`