Question

Please help I need to know how to do it (show work) only #10 and #11

Answer 1

The substitution method works by solving one of the equations for one of the variables (you choose the equation and the variable) and then plugging this back into the other equation, substituying for the chosen variable and solving for the other.

For instance, lets solve problem 10. We have the following system:

`\begin{gathered} 6x-9=y \\ y=-3x \end{gathered}`

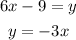
We can see that the "easiest" way to solve them is by substituting the value of y given in the second equation into the first one. It gives

`6x-9=-3x`

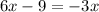
because y=-3x. Now, we must move -3x to the left hand side as +3x. It yields,

`6x+3x-9=0`

since 6x+3x=9x, we have

`9x-9=0`

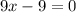
Now, if we move -9 to the left hand side as +9, we obtain

`\begin{gathered} 9x=9 \\ x=(9)/(9) \end{gathered}`

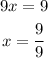
then, x=1. Until now, we solved for x. Now. we must subsitute this value into the second equation. It yields,

`y=-3(1)`

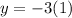
which gives y=-3. Finally, the answer is x=1 and y=-3.

We can check that this is the correct solution by substituting these values into both equations:

`\begin{gathered} 6(1)-9=-3 \\ 6-9=-3 \\ -3=-3\text{ Thats correct!} \end{gathered}`

Now, in the second one, we have

`\begin{gathered} -3=-3(1) \\ -3=-3\text{ Thats correct!} \end{gathered}`

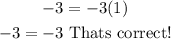
Then our answer is corrrect!