Hello!
First, we have to solve this system, then we can classify it.
Let's solve:

Let's isolate y in the second equation:

Now, let's replace it in the first equation:
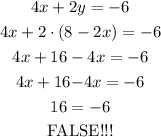
As we can see, this linear system has no solution.
Now, let's classify it:
As this does not admit any solution, we can say that it is inconsistent.