Question

A circular oil slick spreads so that as its radius changes, its area changes. Both the radius r and the area A change with respect to time. If dr/dt is found to be 1.7 m/hr, find dA/dt when r= 39.8 m. Hint: A(r)= πr², and, using the Chain, dA/dt=dA/dr•dr/dt.A) 33.83PI m^2/hrB) 135.32PI m^2/hrC) 67.66PI m^2/hrD) 270.64PI m^2/hr Which is the correct answer?

Answer 1

,As given by the question

There are given that the value

`(dr)/(dt)=1.7\text{ and r=39.8 and A(r)=}\pi(r)^2`

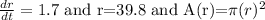
Now,

First find the differentiation of the value of A(r) with respect to r

So,

`\begin{gathered} \text{ A(r)=}\pi(r)^2 \\ \frac{d\text{A(r)}}{dx}=2r\pi \end{gathered}`

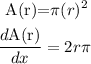
Then,

Put the value of r into the given equation

So,

`\begin{gathered} \frac{d\text{A(r)}}{dt}=2r\pi \\ \frac{d\text{A(r)}}{dt}=2(39.8)\pi \\ \frac{d\text{A(r)}}{dt}=79.6\pi \end{gathered}`

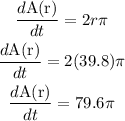
Now,

From the given chain rule

`(dA)/(dt)=(dA)/(dr)*(dr)/(dt)`

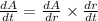
Then,

Put all the values into the above equation

So,

`\begin{gathered} (dA)/(dt)=(dA)/(dr)*(dr)/(dt) \\ (dA)/(dt)=79.6\pi*1.7 \\ (dA)/(dt)=135.32\pi \end{gathered}`

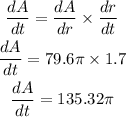
Hence, the correct option is B.