Question

The height in feet of a soccer ball kicked upward from the ground with initial velocity 60 feet per second is modeled by h=-16t^2 + 60t, where t is the time in seconds. Find the time it takes for the ball to return to the ground. find the time it takes for the ball to return to the ground.

Answer 1

Given the equation:

`h=-16t^2+60t`

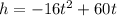
Let's find the time it takes the ball to return to the ground.

When the ball returns to the ground, the height, = 0.

Hence, to find the time it takes the ball to return to the ground, substitute 0 for h and solve for t:

`0=-16t^2+60t`

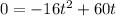
Solving further:

Re-arrange the equation

`-16t^2+60t=0`

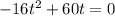
Factor out -4t:

`-4t(4t-15t)=0`

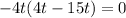
We have the individual factors:

`\begin{gathered} -4t=0 \\ and \\ 4t-15=0 \end{gathered}`

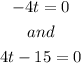
Solve each equation for t:

`\begin{gathered} -4t=0 \\ Divide\text{ both sides by -4:} \\ (-4t)/(-4)=(0)/(-4) \\ \\ t=0 \end{gathered}`

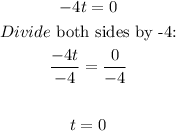
For the second factor:

`\begin{gathered} 4t-15=0 \\ Add\text{ 15 to both sides:} \\ 4t-15+15=0+15 \\ 4t=15 \\ \\ Divide\text{ both sides by 4:} \\ (4t)/(4)=(15)/(4) \\ \\ t=3.75 \end{gathered}`

Therefore it will take 3.75 seconds for the ball to return to the ground.

ANSWER:

3.75 seconds