Question

A 5 cm spring is suspended with a mass of 1.408 g attached to it which extends the spring by 2.078 cm. The same spring is placed on a frictionless flat surface and charged beads are attached to each end of the spring. With the charged beads attached to the spring, the spring's extension is 0.332 cm. What are the charges of the beads? Express your answer in microCoulombs.

Answer 1

First, use the mass of the object attached to the spring and the distance that the spring extends to find the constant of the spring.

Once the spring's constant is known, use it to find the force between the charges of the beads. Finally, use Coulomb's Law to find the charges of the beads.

The force exerted by a spring extended a distance Δx is given by Hooke's Law:

`F=k\Delta x`

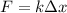
The weight of a mass m is:

`W=mg`

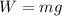
Where g=9.81m/s^2.

Isolate k from the Hooke's Law expression and replace F=W:

`k=(F)/(\Delta x)=(W)/(\Delta x)=(mg)/(\Delta x)`

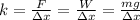
Since the spring extends by 2.078cm when a mass of 1.408g is attached, then:

`\begin{gathered} k=((1.408g)(9.81(m)/(s^2)))/((2.078cm)) \\ \\ =((1.408*10^(-3)kg)(9.81(m)/(s^2)))/((2.078*10^(-2)m)) \\ \\ =0.6647(N)/(m) \end{gathered}`

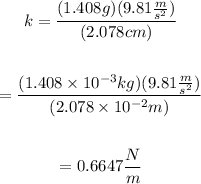
When the charged beads are attached to the ends of the spring, it extends 0.332cm. Then, the force between the charges is:

`F=k\Delta x=(0.6647(N)/(m))(0.332*10^(-2)m)=2.2068*10^(-3)N`

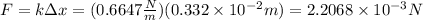
Since the resting length of the spring is 5cm, when the beads are attached, the distance between the beads is 5.332cm.

The force between two charged particles separated a distance r is given by the equation:

`F=k_e(q_1q_2)/(r^2)`

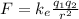
Where k_e is Coulomb's constant:

`k_e=8.98755*10^9N(m^2)/(C^2)`

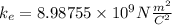
Assuming that both beads have the same charge, isolate q from the equation:

`\begin{gathered} F=k_e(q^2)/(r^2) \\ \\ \Rightarrow q=r\sqrt{(F)/(k_e)} \end{gathered}`

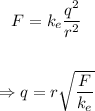
Replace r=5.332cm, F=2.2068*10^-3N and the value of k to find the charge of the beads:

`\begin{gathered} q=(5.332*10^(-2)m)\sqrt{(2.2068*10^(-3)N)/(8.98755*10^9N(m^2)/(C^2))} \\ \\ =26.4211...*10^(-9)C \\ \\ =0.02642\mu C \end{gathered}`

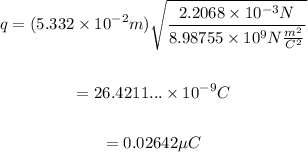
Therefore, the charges of the beads are approximately 0.02642μC if both charges are equal.