Question

A kite is flying 8 feet off the ground it line is pulled taut and cast a 7-ft shadow find the length of the line if necessary round your answer to the nearest 10th

Answer 1

Step-by-step explanation

Since the kite is flying 8 ft from the ground, we can apply the Pythagorean Theorem to obtain the value of the line, by assuming that x represents the unknown value, as shown as follows:

`x^2=8^2+7^2`

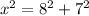
Computing the powers:

`x^2=64+49`

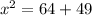
Adding numbers:

`x^2=113`

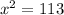
Applying the square root to both sides:

`x=\sqrt[]{113}=10.63014581`

Rounding to the nearest tenth:

`x=10.6`

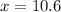
In conclusion, the unknown distance is 10.6 ft