To change from radians to degrees we just need to find a relationship between the two units.
180° (half a turn) is equal to π radians, then, we can multiply 5 radians by the following to change its units:
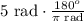
By multiplying by a fraction with 2 equivalent quantities in both numerator and denominator, we keep the 5 radians unaltered while having the equivalent quantity in different units:
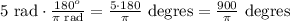
Leaving the answer in terms of π, we have then that 5 radians are equal to 900/π degrees.