Solution
Question A:
- The volume of every prism, whether it is a triangular prism-like the question gives or any other type of prism- is given as
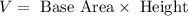
- This means that Shino is correct to say that the volume of the prism is
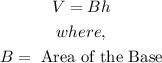
- Thus, Shino is correct.
- However, since the base of the prism is a right triangle with a height of l and a base of w, it means we can further develop Shino's formula by substituting the formula for the area of the triangular base.
- The area of a triangle is
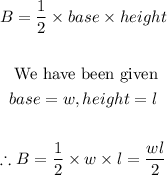
- Thus, if that gives the formula for the base of the triangular prism, then, we can update the formula for the volume of the as follows:
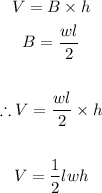
- This is the exact formula that Angelo gets. This means that Angelo is also right
Question B:
- We are given

- Thus, we can find the volume of the prism as follows:
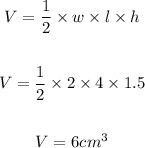
- Thus, the volume of the prism is 6cm³