Question

What is the standard form of the quadratic function that has a vertex at (34)and goes through the point (4.5)?A y=2p - 12x+22B y=x-5x+ 13O cy=+6x+5O R y=x2- 6x+9

Answer 1

To check what is the correct option we can start evaluating which one passes through point 3,4. This is the vertex of the correct equation, so it has to pass through this point. We can evaluate later whether it is the vertex or not, in case it is required.

To check if any option passes through that point, we just need to replace x = 3 and y = 4:

For option A:

`\begin{gathered} y=2x^2-12x+22 \\ 4=2\cdot(3^2)-12\cdot3+22 \\ 4=2\cdot9-36+22 \\ 4=18-14 \end{gathered}`

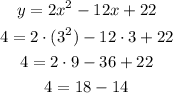
The equation in option A is satisfied. This equation passes through point 3,4. Let's check every other option the same way:

Option B

`\begin{gathered} y=x^2-6x+13 \\ 4=9-6\cdot3+13 \\ 4=9-18+13 \\ 4=4 \end{gathered}`

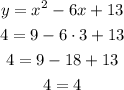
Option B also passes through that point.

Option C:

`\begin{gathered} y=x^2+6x+5 \\ 4=9+6\cdot3+5 \\ 4=9+18+5 \\ 4=32 \end{gathered}`

The equation in option C is not satisfied, does not passes through point 3,4; then we can discard this option.

Option D:

`\begin{gathered} y=x^2-6x+9 \\ 4=9-6\cdot3+9 \\ 4=9-18+9 \\ 4=0 \end{gathered}`

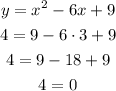
The equation in option D is not satisfied either. We can also discard this option.

The only options passing through point 3,4 are A and B. Now we need to check which one passes also through point 4,5. We can check the same way: replacing 4 where we have x, and 5 where we have y, but this time only for options A and B.

For option A:

`\begin{gathered} y=2x^2-12x+22 \\ 5=2\cdot(4^2)-12\cdot4+22 \\ 5=2\cdot16-48+22 \\ 5=32-26 \\ 5=6 \end{gathered}`

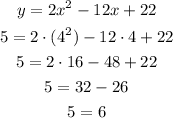
The equation in option A does not pass through point 4,5. The only option left is option B. Let's check it:

`\begin{gathered} y=x^2-6x+13 \\ 5=16-6\cdot4+13 \\ 5=16-24+13 \\ 5=5 \end{gathered}`

The equation in option B passes through point 4,5.

If we had more than one option left, we would need which one has the vertex exactly at 3,4. However, we have proved that the only option that passes through both points (3,4 and 4,5) is option B. Then, that is the correct answer.

The correct answer is option B.