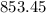Answer:
The product of CM and MB is;
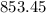
Step-by-step explanation:
Given that the length of each sides of the equilateral triangle is

So, the length CB equals 50.6.
Since AD is a bisector then the length CD would be;
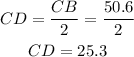
Also, the triangle CDM formed by the bisectors is a right angled triangle.
Since line CE bisect angle ACB.
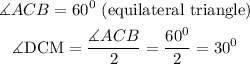
We can then calculate the length of line MB and CM;
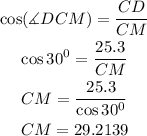
And since it is an equilateral triangle;
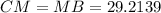
So;
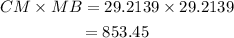
Therefore, the product of CM and MB is;