Question

A toy maker produces wooden trains and wooden airplanes. Each train requires 3 ounces of paint and each airplane requires 5 ounces of paint. The toy maker has a gallon can of paint (64 ounces). If he wants to use it to paint 14 toys, how many of each can he paint?

Answer 1

Let be "t" the number of wooden trains that he can paint and "a" the number of wooden airplanes he can paint.

Based on the information given in the exercise, you can set up the following System of equations:

`\begin{cases}t+a=14 \\ 3t+5a=64\end{cases}`

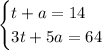
You can solve it using the Substitution method:

1. You can solve for "a" from the first equation:

`a=14-t`

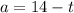
2. Substitute the new equation into the second equation.

3. Solve for "t".

Then:

`\begin{gathered} 3t+5a=64 \\ 3t+5(14-t)=64 \\ 3t+70-5t=64 \\ -2t=64-70 \\ \\ t=(-6)/(-2) \\ \\ t=3 \end{gathered}`

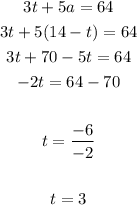
4. Substitute the value of "t" into any original equation.

5. Solve for the variable "a".

Then:

`\begin{gathered} t+a=14 \\ 3+a=14 \\ a=14-3 \\ a=11 \end{gathered}`

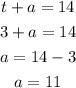
The answer is: He can paint 3 trains and 11 airplanes.