Given:
the distance of the tortoise is,
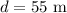
The coefficient of friction between the tyre and the asphault is,
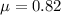
The acceleration of the transport is,
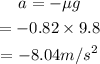
Now the final velocity after the brakes applied is 0.
we have to find the initial velocity.
we can write,
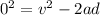
Substituting the values we get,
![\begin{gathered} 0^2=v^2-2*8.04*55 \\ v=\sqrt[]{2*8.04*55} \\ v=29.7\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/ur0y164stgkla4gimnb2o20tz3g996u4pn.png)
Hence the speed limit is 29.7 m/s.