92 adult tickets were sold
230 child tickets were sold
Step-by-step explanation
Step 1
set the equations
let x represents the number of adult tickets sold
let y represents the number of child tickets sold
cost of adult ticket: 12
cost for child ticket : 5
so
a)On the first day of the fair, 322 tickets were sold
so
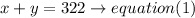
b)total of $2,254
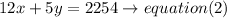
Step 2
Solve the equations:
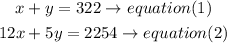
a) isolate x in equation (1) and then replace in eqaution(2)
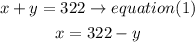
replace in equation (2)

b) now, replace the y value in equation (1) and solve for x

therefore
92 adult tickets were sold
230 child tickets were sold
I hope this helps you