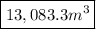Answer:
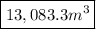
Step-by-step explanation:
Step 1. The information we have about the cone is:

Step 2. To find the Volume of the cone, we use the following equation:
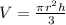
Where V is the volume, r is the radius and π=3.14.
To find r, we use:
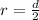
The value of the radius is:
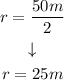
Step 3. Substitute all of the values into the formula to find the Volume:
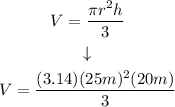
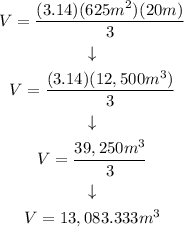
Solving the operations step by step:
Rounding to the nearest tenth (1 decimal):
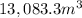
Answer: