Question

Find a polynomial f(x) of degree 3 with real coefficients and the following zeros. -3,2-i f(x)=

Answer 1

We have to find a 3rd degree polynomial with real coefficients and the zeros -3 and 2-i.

We have one of the zeros that is a complex number. For the polynomial to have real coefficients, the conjugate of 2-i also has to be a zero of the polynomial.

Then, 2+i is also a zero of the polynomial.

Then, we can write the polynomial in the factorized form as:

`f(x)=(x+3)(x-(2-i))(x-(2+i))`

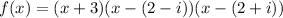
We then can expand the factors using the distributive property:

`\begin{gathered} f(x)=(x+3)(x-2+i))(x-2-i)) \\ f(x)=(x+3)((x-2)^2-i^2) \\ f(x)=(x+3)((x-2)^2-(-1)) \\ f(x)=(x+3)(x^2-4x+4+1) \\ f(x)=(x+3)(x^2-4x+5) \\ f(x)=x^3-4x^2+5x+3x^2-12x+15 \\ f(x)=x^3-x^2-7x+15 \end{gathered}`

We can graph this polynomial as:

We can see that it only has one real root at x = -3. The other two roots are complex roots.

Answer: f(x) = x³ - x² - 7x + 15