Question

The two-way frequency table below shows how many students passed their driving test aswell as the number who took a preparatory class. Find the probability that a student passedthe test, given that he or she took the class.Passed82Failed33ClassNo class232133115o8211582159oNone of the other answers are correct

Answer 1

Option B is correct.

The probability that a student passes the test given that he or she took the class = P(A | B) = (82/115)

Step-by-step explanation

The probability that a student passes the test given that he or she took the class is called conditional probability.

In conditional probability, the probability that event A occurs given that event B has already occured is presented as P(A | B) and it is given mathematically as

P(A | B) = P(A n B) ÷ P(B)

For this question, we are asked to find the probability that a student passes the test given that he or she took the class

The probability that a student passes the test

= P(A) = (82 + 23) ÷ (82 + 33 + 23 + 21) = (105) ÷ (159) = (105/159) = (35/53) = 0.6604

The probability that a student took the class

= P(B) = (82 + 33) ÷ (82 + 33 + 23 + 21) = (115) ÷ (159) = (115/159) = 0.7233

The probability that a student passes the test and took the class

= P(A n B) = (82) ÷ (82 + 33 + 23 + 21) = 82 ÷ 159 = (82/159) = 0.5157

The probability that a student passes the test given that he or she took the class = P(A | B) = P(A n B) ÷ P(B) = (82/159) ÷ (115/159)

`\begin{gathered} P(A|B)=(82)/(159)/(115)/(159) \\ =(82)/(159)*(159)/(115) \\ =(82)/(115) \end{gathered}`

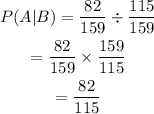
P(A | B) = (82/115)

Hope this Helps!!!