Question

A roller coaster features a near vertical drop of 140 meters. Assuming that friction and air resistance are negligible, and that the initial velocity was zero, what would be the speed at the bottom of the drop?48 m/s52 m/s42 m/s35 m/s

Answer 1

52 m/s

Step-by-step explanation:

By the conservation of energy, the potential energy at the top will be equal to the kinetic energy at the bottom, so

`\begin{gathered} E_i=E_f_{}_{} \\ PE_i=KE_f_{} \\ \text{mgh}=(1)/(2)mv^2 \end{gathered}`

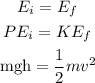
Where m is the mass, g is the gravity, h is the height and v is the speed. Solving for the speed v, we get:

`\begin{gathered} 2\text{mgh}=mv^2 \\ \frac{2\text{mgh}}{m}=v^2 \\ 2gh=v^2 \\ v=\sqrt[]{2gh} \end{gathered}`

Then, replacing g = 9.8 m/s² and h = 140 m, we get:

`\begin{gathered} v=\sqrt[]{2(9.8)(140)} \\ v=52.38\text{ m/s} \end{gathered}`

Therefore, the answer is 52 m/s