Question

Find all points (x,y) where the tangent line to f(x)=3x^2 +6x is horizontal.

Answer 1

Given:

The equation of a function is,

`f(x)=3x^2+6x`

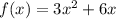
The objective is to find the point where the tangent line will be horizontal.

Step-by-step explanation:

The tangent line can be horizontal at the point where the slope value is zero.

The slope of the curve can be calculated by differentiating the equation.

To find derivative:

Let's differentiate the given function and equate to zero.

`\begin{gathered} (d)/(dx)(f(x))=(d)/(dx)(3x^2+6x) \\ 0=3(2x)+6(1) \\ 0=6x+6\text{ . . . . . (1)} \end{gathered}`

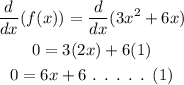
To find x :

On further solving the equation (1),

`\begin{gathered} 0=6x+6 \\ 6x=-6 \\ x=(-6)/(6) \\ x=-1 \end{gathered}`

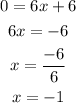
To find the (x,y):

Substitute the value of x in the given equation.

`\begin{gathered} y=3x^2+6x \\ y=3(-1)^2+6(-1) \\ y=3(1)-6 \\ y=-3 \end{gathered}`

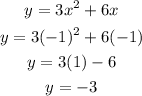
Thus, the obtained coordinate is (-1,-3).

Hence, the tangent line is horizontal at the point (x,y) = (-1,-3).