Question

Find the perimeter of the triangle to the nearest tenth of a meter.

Answer 1

You can identify that the triangle shown in the picture is a Right triangle.

You can use the following Trigonometric Identity:

`\tan \alpha=(opposite)/(adjacent)`

In this case:

`\begin{gathered} \alpha=30\degree \\ opposite=5 \\ adjacent=x \end{gathered}`

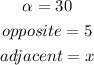
See the picture below:

Substitute values into

`\tan \alpha=(opposite)/(adjacent)`

And solve for "x":

`\begin{gathered} \tan (30\degree)=(5)/(x) \\ \\ x\tan (30\degree)=5 \\ \\ x=(5)/(\tan(30\degree)) \\ \\ x=5\sqrt[]{3} \end{gathered}`

To find the length of the hypotenuse, you can use the Pythagorean theorem:

`a^2=b^2+c^2`

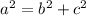
Where "a" is the hypotenuse and "b" and "c" are the legs of the Right triangle.

In this case:

`\begin{gathered} a=y \\ b=5 \\ c=5\sqrt[]{3} \end{gathered}`

Substituting values into the equation and solving for the hypotenuse, you get that this is:

`\begin{gathered} y^2=(5)^2+(5\sqrt[]{3})^2 \\ y=25+25(3) \\ y=\sqrt[]{100} \\ y=10 \end{gathered}`

The perimeter of a triangle can be found by adding the lengths of its sides. Then, the perimeter of this triangle rounded to the nearest tenth, is:

`\begin{gathered} P=5m+5\sqrt[]{3}m+10m \\ P=23.66m \\ P\approx23.7m \end{gathered}`

The answer is: Option C.