Step-by-step explanation
From the statement, we have an arithmetic sequence with:
• common difference d = 4,
,
• 3rd term a₃ = 19.
We must find the 77th term.
(1) The general formula for the nth term of an arithmetic sequence is:
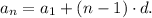
Replacing the data from above, we have:
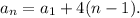
(2) We compute the a₁. Replacing the n = 3 and a₃ = 19, we have:
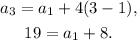
Solving for a₁, we get:

Replacing this value in the general formula, we have:

(3) Evaluating the general formula for n = 77, we get the 77th term of the sequence:
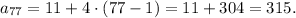
Answer
a₇₇ = 315