Question

A student receives scores of 85, 78 and 81 on his first 3 exams in algebra. What is the lowest score the student has to get on his fourth exam, so his test average would be at least an 84?

Answer 1

The student's scores in his first three exams are 85, 78, and 81.

You have to find what score is needed on a fourth exam to have an average grade of at least 84 points.

To determine the average score of 4 exams, you have to add each score and divide it by the number of exams, following the formula:

`\bar{X}=(\sum ^n_1x_i)/(n)`

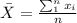
Where

xi represents each observation of the sample, in this exercise, it represents the score of each test.

n represents the same size, in this exercise, is the number of algebra tests

We know that:

The average is 84 points

n= 4 tests

Three observations are 85, 78, 81

If "x" represents the score of the fourth Test, then the calculation of the average grade can be expressed as:

`84=(85+78+81+x)/(4)`

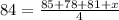
From this expression, you can determine the value of x

-Solve the sum on the denominator:

`84=(244+x)/(4)`

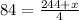
-Multiply both sides by 4

`\begin{gathered} 84\cdot4=4\cdot(244+x)/(4) \\ 336=244+x \end{gathered}`

-Subtract 244 from both sides

`\begin{gathered} 336-244=244-244+x \\ 92=x \end{gathered}`

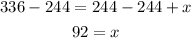
This means that the student needs at least 92 points on the fourth test, for his average score to be at least 84 points.