Question

The distance that a free falling object falls is directly proportional to the square of the time it falls (before it hits the ground). If an object fell 91 ft in 2 seconds, how farwill it have fallen by the end of 6 seconds? (Leave the variation constant in fraction form or round to at least 2 decimal places. Round your final answer to the nearestfoot.)

Answer 1

Let 'd' represent the distance.

Let 't' represent the time.

Given that:

`d\propto t^2`

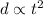
Introducing a constant 'k'

`d=kt^2`

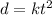
where,

`\begin{gathered} d=91ft \\ t=2seconds \end{gathered}`

Therefore,

`\begin{gathered} 91=k*2^2 \\ 91=k*4 \\ Divide\text{ both sides by 4} \\ (91)/(4)=(k*4)/(4) \\ \therefore k=(91)/(4)=22.75 \end{gathered}`

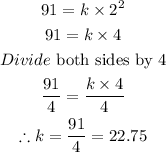
Hence, the relationship connecting the distance and the time is,

`d=22.75t^2`

Let us now solve for the distance if the time is 6seconds.

`\begin{gathered} d=22.75*6^2=819 \\ \therefore d=819feet \end{gathered}`

Hence, the answer is 819 feet.