Consider the given polynomial,
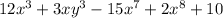
1.
In its standard form, the terms of a polynomial are written in decreasing order of its exponents. So the standard form for the given polynomial (based on x) is given by,

2.
The leading term is,

Removing the variable part, the remaining is referred as the coefficient of that term.
So the coefficient of the leading term is 2.
3.
The constant is the last term in the standard form.
The constant term can also be understood as the term of the polynomial that does not contain the variable 'x'.
In the given polynomial, note that the first 4 terms contain the variable 'x' in their expression. While it is the 5th i.e. the last term that is free from all variables. So this 5th term will be the constant term.
The value of this 5th term is 10.
Therefore it can be concluded that the constant term is 10.
4.
The degree of the polynomial is the value of the exponent of the variable appearing in the leading term (i.e. the highest-powered term).
It can simply be understood as the largest value of the exponent of variable appearing in the polynomial.
Observe that the largest exponent of the variable is seen in the leading term as 8.
Therefore, the degree of the polynomial is 8.