Given:
The inductance is,
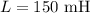
The current is,
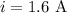
The frequency of the current is,
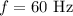
To find:
The phase angle between the current and the voltage
Step-by-step explanation:
The phase angle between the current and the voltage is,
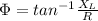
As the circuit is purely inductive,
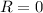
The phase angle is,
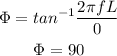
Hence, the phase angle is 90 degrees.