Question

A spherical weather balloon has a volume of 12.0 dm3 when inflated at STP. Assuming it could stay anchored and intact, as a hurricane passed overhead lowering the pressure to 720 mm Hg, what would be the new volume of the balloon assuming the temperature stays at 0°C?

Answer 1

The final volume of the balloon is 12.67L

Step-by-step explanation

Given that;

The initial volume of the ballon is 12dm^3

The initial temperature at STP is 273.15 degrees Celcius

The initial pressure at STP is 760 mmHg

The final temperature is 0 degrees Celcius

The final volume is 720 mmHg

Follow the steps below to find the new volume of the balloon

Step1; Write the general gas law equation

`\text{ }\frac{\text{ P1 V1}}{\text{ T1}}=\text{ }\frac{\text{ P2V2}}{\text{ T2}}`

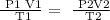
Step 2; Convert the volume and temperature to liters and degrees Kelvin

`\begin{gathered} \text{ 1dm}^3\text{ }=\text{ 1L} \\ \text{ Hence, 12dm}^3\text{ is equivalent to 12L} \\ \\ \text{ The final temperature is 0}\degree C \\ \text{ T = t + 273.15} \\ \text{ T = 0 + 273.15} \\ \text{ T = 273.15K} \end{gathered}`

Step 3; Substitute the given data into the formula above to find the final volume

`\begin{gathered} \text{ }\frac{\text{ P1V1}}{\text{ T1}}\text{ }=\text{ }\frac{\text{ P2 V2}}{\text{ T2}} \\ \\ \text{ }\frac{760*\text{ 12}}{273.15}\text{ }=(720* V2)/(273.15) \\ \text{ Cross multiply} \\ \text{ 760 }*\text{ 12 }*\text{ 273.15 }=\text{ 720 }*\text{ V2 }*\text{ 273.15} \\ \text{ Isolate V2} \\ \text{ V2 }=\text{ }\frac{760\text{ }*\text{ 12}*\text{ 273.15}}{720\text{ }*\text{ 273.15}} \\ \text{ } \\ \text{ V2}=\frac{760*12*\cancel{273.15}}{720*\cancel{273.15}} \\ \text{ } \\ \text{ V2 }=\text{ }(9120)/(720) \\ \text{ V2 = 12.67L} \end{gathered}`

Hence, the final volume of the balloon is 12.67L