Question

Hello! Was able to figure out everything on this problem besides the slant asymptotes and types of discontinuities. Thanks for your help!

Answer 1

• The slant asymptote is y=x-3.

,

• The function g(x) has a removable discontinuity at x=-1.

,

• The function g(x) has a non-removable discontinuity at x=2.

Explanation:

Given that the function, f(x) has zeros of 8, -1, and -3.

Then, by the factor theorem:

`f(x)=(x-8)(x+1)(x+3)`

If we divide the f(x) by x²-x-2:

`\begin{gathered} g(x)=(f(x))/(x^2-x-2)=((x-8)(x+1)(x+3))/(x^2-2x+x-2) \\ =((x-8)(x+1)(x+3))/(x(x-2)+1(x-2)) \\ =((x-8)(x+1)(x+3))/((x+1)(x-2)) \\ =((x-8)(x+3))/(x-2) \end{gathered}`

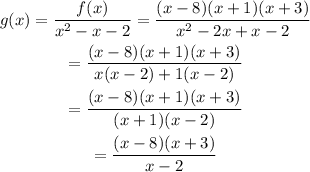
Therefore, the rational function, g(x) in simplest form is:

`g(x)=((x-8)(x+3))/(x-2)`

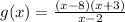
Since the degree of the numerator is one degree greater than the degree of the denominator, a slant asymptote exists. To find this, divide the numerator by the denominator:

`g(x)=(x^2+3x-8x-24)/(x-2)=(x^2-5x-24)/(x-2)`

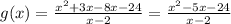
The quotient of the division is x-3 with a remainder of 18.

The slant asymptote is y=x-3.

Given g(x) in the form below:

`g(x)=((x-8)(x+1)(x+3))/((x+1)(x-2))`

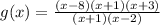
Set the denominator equal to 0 to find the point of discontinuities.

`\begin{gathered} (x+1)(x-2)=0 \\ x+1=0\text{ or }x-2=0 \\ x=-1,x=2 \end{gathered}`

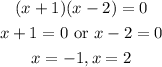
The function is discontinuous at x=-1 and x=2.

However, notice that there is a common factor in the numerator and the denominator, x+1. The zero for this factor is x = -1 . Therefore:

• The function g(x) has a removable discontinuity at x=-1.

• The function g(x) has a non-removable discontinuity at x=2.