r and p = true
s and t = false
The logical expression is given by
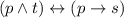
Let us solve the above expression.
(p ∧ t) means p and t
(p ∧ t) is true if p and t both are true.
But we know that both p and t are not true since t is false.
So, (p ∧ t) is false.
(p -> s) means p implies s
(p -> s) is true if p is false or s is true.
But we know that p is true and s is false.
This means that (p -> s) is false.
Finally,
↔ means equivalent
(p ∧ t) ↔ (p -> s) is true if both are true or both are false.
We know that (p ∧ t) is false and (p -> s) is false
So, (p ∧ t) ↔ (p -> s) is true since both of them are false.