To solve this question, we can substitute the given point into the inequalities. That is, by substituying x=2 and y=-3 into the first inequality, we obtain
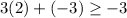
and the left hand side is equal to 6-3=3. Because 3>-3, the point (2,-3) can be a solution. However, we must be the same for the remaining inequality, that is, by substituying x=2 and y=-3 into the second inequality, we have
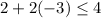
and the left hand side is equal to 2-6=-4, then -4<4.
With both results, we can conclude that the point (2,-3) is a solution of the system.