SOLUTION
The question provides us with a right-angled triangle and we know the adjacent to be 3 and the oppoisite to be 7.
With this set of values, it is clear that the best way to solve this question is using PYTHAGORAS THEOREM
The Pythagoras theorem is shown below:
Given the below right-triangle
The Pythagoras theorem is given as
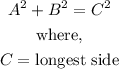
Thus, using the Pythagoras theorem described above, we can solve the problem, with the longest side, in this case, being x.
This is done below:
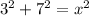
Let us solve the above equation by finding the value of x
![\begin{gathered} 3^2+7^2=x^2 \\ 9+49=x^2 \\ 58=x^2 \\ \text{ Find the square root of both sides} \\ \sqrt[]{58}=\sqrt[]{x^2} \\ \sqrt[]{58}=x \\ \\ \therefore x=\sqrt[]{58}\text{ } \\ \\ \text{Thus, the final answer is OPTION B} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zsfeqmxu4oktx8i16rqzrqexqn5nd9rgbp.png)