To answer this question we need to recall the expression for the square of a binomial:
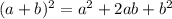
We are given the following expression
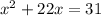
Comparing to the general formula, we note the first term is similar to the term a^2
This means we already have the square of the first term, i.e. a = x
Now we focus on the second term 22x. It must be equal to the expression 2ab, that is
22x = 2ab
Since we already know a = x, then
22x = 2xb
Simplifying by x, we get
22 = 2b
Dividing by 2:
b = 11
It means the second term of the square is 11 and it's missing from the expression on the left side of the equation.
Completing square means we must add the exact number to form the square of the binomial as needed.
Note the missing term is b^2, the square of 11. Since 11 * 11 = 121, we add 121 to both sides of the equation:
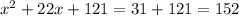
The left side is already formed as the square of (x+11), thus the required expression is
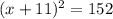
Correct option: D.