Question

The height of a soccer ball that is kicked from the ground canbe approximated by the function:y = -14x2 + 42xwhere y is the height of the soccer ball in feet x seconds after it is kicked.Find the time it takes the soccer ball to reach its maximum height in seconds:

Answer 1

To solve this question you have to apply the first and second derivative criteria. First we are going to derive the equation

`\begin{gathered} y^(\prime)\text{ = -28x +42} \\ \text{now we put y'=0 to find the critical points} \\ -28x\text{ +42 =0 } \\ x=(-42)/(-28)=\text{ 1.5} \end{gathered}`

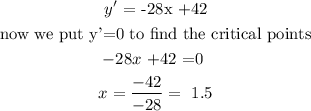
Since

`y^(\doubleprime)\text{ =-28 }`

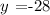
by the second derivative criteria, we know that y reaches a maximum at x=1.5. Then it takes 1.5 seconds to reach the maximum height.