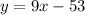Question

Consider the line x+9y= -5Find the equation of the line that is parallel to this line and passes through the point (6, 1)Find the equation of the line that is perpendicular to this line and passes through the point (6, 1) Equation of the parallel line: Equation of the perpendicular line:

Answer 1

Answer: y=1/9x+5/3

Explanation:

Answer 2

We want to write a parallel line and another perpendicular to

`x+9y=-5`

That passes through the point (6, 1).

Parallel lines have the same slope. To determinate the slope of our line, let's rewrite it in slope intercept form. The slope intercept-form is

`y=mx+b`

Where m represents the slope and b represents the y-intercept.

Rewritting our line:

`\begin{gathered} x+9y=-5 \\ 9y=-x-5 \\ y=-(x)/(9)-(5)/(9) \end{gathered}`

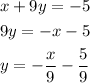
The slope of this line is -1/9.

The set of parallel lines, since they have the same slope, have the following form

`y=-(x)/(9)+c`

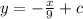
The y-intercept of our desired parallel line can be determinated by using the point we know that it belongs to the parallel line. Making the substitution, we have

`\begin{gathered} 1=-(6)/(9)+c \\ \Rightarrow c=(15)/(9)=(5)/(3) \end{gathered}`

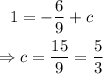
The equation for the parallel line is:

`y=-(x)/(9)+(5)/(3)`

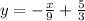
For the perpendicular line, the idea is almost the same. The difference is the slope is not the same, it is minus the inverse of our line.

`m_(\perp)=-(m)^(-1)\Rightarrow m_(\perp)=-((-1)/(9))^(-1)=9`

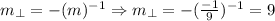
The set of perpendicular lines is

`y=9x+d`

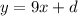
The y-intercept of our desired pperpendicular line can be determinated by using the point we know that it belongs to the perpendicular line. Making the substitution, we have

`\begin{gathered} 1=9*6+d \\ 1=54+d \\ d=-53 \end{gathered}`

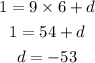
The equation for the perpendicular line is:

`y=9x-53`