The equation of a line with slope m that passes thorugh the point (x1,y1) is given as:

Plugging the values we know we have:
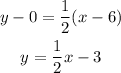
Therefore the equation of the line is:
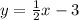
To find the graph we need another point. If x=0, then:
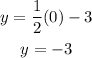
Then we have the point (0,3). Plotting the points (0,3) and (6,0) and join them with a straign