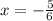Question

Hi, I need help solving this equation using the 'Product Rule', thanks

Answer 1

Given:

`y=2x(x+3)^2`

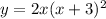
Where:

Gradient = 14

Let's find the exact values of x for which the gradient of the tangent line to the curve is 14.

Let's first simplify the equation:

`y=2x((x+3)(x+3))`

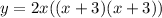
Expand using the FOIL method:

`\begin{gathered} y=2x(x(x+3)+3(x+3)) \\ \text{ } \\ \text{ Apply distributive property:} \\ y=2x((x(x)+x(3)+3(x)+3(3)) \\ \\ y=2x(x^2+3x+3x+9) \\ \\ y=2x(x^2+6x+9) \\ \\ y=2x(x)+2x(6x)+2x(9) \\ \\ y=2x^3+12x^2+18x \end{gathered}`

Now, let's find the first derivative of the equation:

`\begin{gathered} (d)/(dx)(y)=(d)/(dx)(2x^3+12x^2+18x) \\ \\ y^(\prime)=6x^2+24x+18 \end{gathered}`

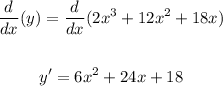
Set the derivative to 14 and solve for x.

We have:

`y^(\prime)^(\prime)=12x+24`

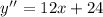
Now, set the second derivative to 14:

`12x+24=14`

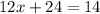
Solve for x:

Subtract 24 from both sides:

`\begin{gathered} 12x+24-24=14-24 \\ \\ 12x=-10 \\ \\ x=-(10)/(12) \\ \\ x=-(5)/(6) \end{gathered}`

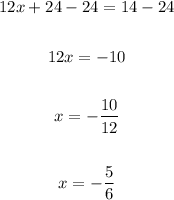
Therefore, the exact value of x for which the gradient of the tangent to the curve is given is:

`-(5)/(6)`

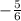
ANSWER:

`x=-(5)/(6)`