To use the Midpoint Rule, we need to divide the interval [0, 4] into 4 equal intervals. This give us 4 intervals of width 1 unit, which are the base of the rectangles.
The intervals are:
[0, 1], [1, 2], [2, 3], [3, 4]
And find the midpoint of each interval:
[0, 1] : 0.5
[1, 2] : 1.5
[2, 3] : 2.5
[3, 4] : 3.5
Now, we need to evaluate the function on each midpoint of each interval, which will act as the height of each rectangle:
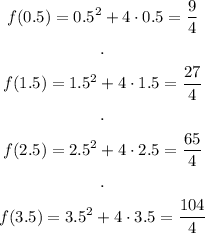
And now, we calculate the area of each rectangle:
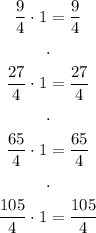
Finally, we add all the areas and get the midpoint approximation:
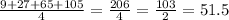
By the Midpoint Rule approximation, the area under the curve of f(x) in the interval [0, 4] is 51.5