From the given table and options, we can note a linear behavior. Lets find the slope m and the y-intercept b for our table. As we know the line equation is

where the slope m is given by

where the values on the right hand side come from 2 points of our table, for instance, we can choose points
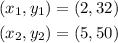
by substtuting these values into the slope formula, we get

which gives
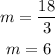
then, our line equation has the form
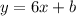
In order to find b, we must substitute one of the 2 choosen points, if we substitute point (2,32), we get
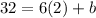
then, we have
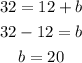
then, the searched line is
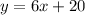
which corresponds to the last option