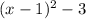Question

Question 3(Multiple Choice Worth 1 points)(08.02 LC)Complete the square to transform the expression x2 – 2x – 2 into the form a(x – h)2 + k.(x - 1)2 + 3(x - 1)2 - 3(x - 2)2 - 3(x - 2)2 + 3

Answer 1

We need to add and subtract the same number in the expression so we can write it as a square and a constant, as in the following expression:

`a\left(x-h\right)^2+k`

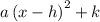
The given expression is:

`x^2-2x-2`

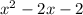
In order to find the number that must be added and subtracted, let's expand the general expression:

`\begin{gathered} a(x-h)^(2)+k \\ \\ a(x^2-2hx+h^2)+k \\ \\ ax^2-2ahx+ah^2+k \end{gathered}`

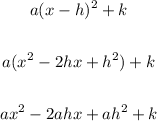
Comparing the coefficients of the general and the given expression, we have:

`\begin{gathered} x^(2)-2x-2 \\ \\ ax^(2)-2ahx+ah^(2)+k \\ \\ x^2=ax^2\Rightarrow a=1 \\ \\ -2x=-2ahx=2hx\Rightarrow h=1 \\ \\ -2=ah^2+k=1+k\Rightarrow k=-3 \end{gathered}`

So, using a = 1, h = 1, and k = -3, we can write:

`x^2-2x-2=1(x-1)^2-3=(x-1)^2-3`

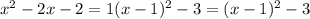
Notice that we obtain the same result by adding 3-3 to the original expression:

`x^2-2x-2=x^2-2x-2+3-3=(x^2-2x+1)-3=(x-1)^2-3`

Therefore, the answer is:

`\begin{equation*} (x-1)^2-3 \end{equation*}`