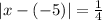Question

Describe all numbers x that are at a distance of 14 from the number −5. Express this using absolute value notation.

Answer 1

The distance (d) between two numbers a and b equals the absolute value of their difference:

`d=|a-b|`

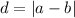
If a number x is at a distance of 1/4 from the number -5, then:

`|x-(-5)|=(1)/(4)`

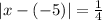
Solve for x. Remember that when an equation involves a variable inside an absolute value, two cases must be considered: If the expression inside the absolute value is positive or if it is negative.

Case 1: x-(-5) is positive.

Then:

`|x-(-5)|=x-(-5)`

Solve for x:

`\begin{gathered} |x-(-5)|=(1)/(4) \\ \Rightarrow x-(-5)=(1)/(4) \\ \Rightarrow x+5=(1)/(4) \\ \Rightarrow x=(1)/(4)-5 \\ \therefore x=-(19)/(4) \end{gathered}`

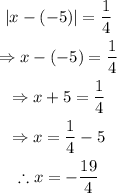
Case 2: x-(-5) is negative.

Then:

`|x-(-5)|=-(x-(-5))`

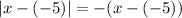
Solve for x:

`\begin{gathered} |x-(-5)|=(1)/(4) \\ \Rightarrow-(x-(-5))=(1)/(4) \\ \Rightarrow-(x+5)=(1)/(4) \\ \Rightarrow x+5=-(1)/(4) \\ \Rightarrow x=-(1)/(4)-5 \\ \therefore x=-(21)/(4) \end{gathered}`

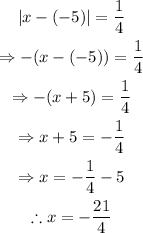
Therefore, all the numbers that are at a distance of 1/4 from the number -5 are -21/4 and 19/4. They can be described by the equation:

`|x-(-5)|=(1)/(4)`