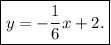Question

3. Which of the following equations is perpendicular to the line 6x – 3y =3 andpasses through the point (6, 1)?

Answer 1

Explanation :

We first write the equation given in the slope-intercept form:

`6x-3y=3`

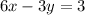
subtracting 6x from both sides gives

`\begin{gathered} -3y=3-6x \\ \end{gathered}`

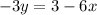
Finally, dividing both sides by -3 gives

`y=(3-6x)/(-3)`
`y=6x-1`

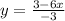
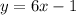
Now, we have to recall at this point that if a linear equation is written in the form

`y=mx+b`

then a perpendicular line has the equation

`y=-(1)/(m)x+c`

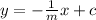
where c is a constant that satisfies any given conditions.

Therefore, in our case, the equation of the perpendicular line is

`y=-(1)/(6)x+c`

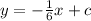
We are told that this line passes through (6, 1); therefore, it must satisfy the conditions that at x = 6, y = 1:

`1=-(1)/(6)(6)+c`
`\begin{gathered} 1=-1+c \\ \boxed{c=2.} \end{gathered}`

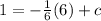
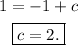
Hence, the equation of a perpendicular line that passes through (6, 1) is

`\boxed{y=-(1)/(6)x+2.}`