We know that:
• If the two lines have different slopes, the system has exactly one solution.
,
• If the two lines have the same slope and y-intercept, the system has infinite solutions.
,
• If the two lines have the same slope and different y-intercepts, they are parallel, and the system has no solutions.
Then, we need to know the slopes of the lines.
• Line 1
We write the equation in its slope-intercept form. For this, we solve the equation for y.
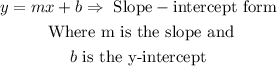
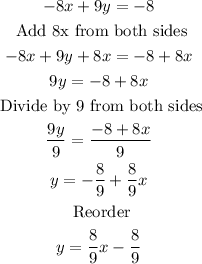
Then, the slope of this line is 8/9.
• Line 2
As we can see, this line is already in its slope-intercept form.
Then, the slope of this line is -6/7.
Since the lines have different slopes, the system has exactly one solution.