Question

QUESTION 1 1 POINTUse slopes to determine if the lines -6x + 8y = 2 and -8x+ 6y = 1 are perpendicular.

Answer 1

Recall that the equation of a line in slope-intercept form is given by

`y=mx+b`

Where m is the slope and b is the y-intercept.

Let us re-write the given equations into the slope-intercept form to identify their slopes.

`\begin{gathered} -6x+8y=2 \\ 8y=6x+2 \\ y=(6x)/(8)+(2)/(8) \\ y=(3x)/(4)+(1)/(4) \end{gathered}`

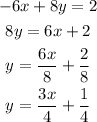
So, the slope of the 1st equation is 3/4

`m_1=(3)/(4)`

Now, the 2nd equation becomes,

`\begin{gathered} -8x+6y=1 \\ 6y=8x+1 \\ y=(8x)/(6)+(1)/(6) \\ y=(4x)/(3)+(1)/(6) \end{gathered}`

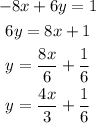
So, the slope of the 2nd equation is 4/3

`m_2=(4)/(3)`

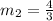
Recall that two equations are perpendicular if their slopes are negative reciprocal of each other.

Mathematically,

`m_2=-(1)/(m_1)`

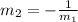
Substitute the values of the slopes and check if the relation holds true.

`\begin{gathered} (4)/(3)=-(1)/((3)/(4)) \\ (4)/(3)\\e-(4)/(3) \end{gathered}`

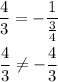
As you can see, the relation does not hold true since one is positive and the other is negative.

Therefore, we can conclude that the given equations are not perpendicular.