The correct option is a.
The correct system of linear equations that can be solved using the given equation is:
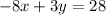
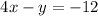
To determine which system of linear equations can be solved using the given equation
![$\left[\begin{array}{l}x \\ y\end{array}\right]=\left[\begin{array}{cc}(1)/(4) & (3)/(4) \\ 1 & 2\end{array}\right]\left[\begin{array}{c}28 \\ -12\end{array}\right]$](https://img.qammunity.org/2023/formulas/mathematics/college/6dvprv04y9r1k91tr2mzbmd9ojx82mzvu8.png) , let's perform matrix multiplication to find the values of x and y:
, let's perform matrix multiplication to find the values of x and y:
![$\left[\begin{array}{l}x \\ y\end{array}\right]=\left[\begin{array}{cc}(1)/(4) & (3)/(4) \\ 1 & 2\end{array}\right]\left[\begin{array}{c}28 \\ -12\end{array}\right]$](https://img.qammunity.org/2023/formulas/mathematics/college/6dvprv04y9r1k91tr2mzbmd9ojx82mzvu8.png)
Step 1: Multiply the matrices.
![$\left[\begin{array}{l}x \\ y\end{array}\right]=\left[\begin{array}{cc}(1)/(4) & (3)/(4) \\ 1 & 2\end{array}\right]\left[\begin{array}{c}28 \\ -12\end{array}\right] = \left[\begin{array}{c}(1)/(4) \cdot 28 + (3)/(4) \cdot (-12) \\ 1 \cdot 28 + 2 \cdot (-12)\end{array}\right]$](https://img.qammunity.org/2023/formulas/mathematics/college/k0lyy57mvdl175q1ufbuygkjo9xtdyecfv.png)
Step 2: Calculate the values.
![$\left[\begin{array}{l}x \\ y\end{array}\right]=\left[\begin{array}{c}7 - 9 \\ 28 - 24\end{array}\right] = \left[\begin{array}{c}-2 \\ 4\end{array}\right]$](https://img.qammunity.org/2023/formulas/mathematics/college/w8f2lo8ytlt9get868fzk9qovfr0iacjx2.png)
So, the values of x and y are
 and
and
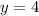 .
.
Now, let's check which system of equations corresponds to this solution.
System 1:
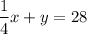
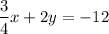
Plugging in the values we found:
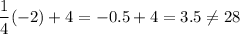 (Not true)
(Not true)
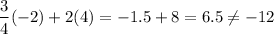 (Not true)
(Not true)
System 2:
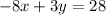
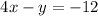
Plugging in the values we found:
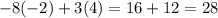 (True)
(True)
 (True)
(True)