Step-by-step explanation
Two vectors are orthogonal if the dot product of the vectors is zero. On the other hand, the dot product of two vectors is defined as follows:
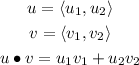
So, let us calculate the dot product of the given vectors:
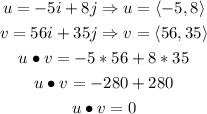
As we can see, the dot product of the given vectors is zero. Therefore, the vectors are orthogonal.
Answer
The vectors are orthogonal because u · v = 0.