Interior angles of a triangle add up to 180, this imply that
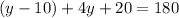
Now, by combining similar terms, we have
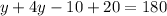
which gives
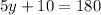
If we movw +10 to the right hand side as -10, we obtain
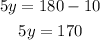
then, y is equal to
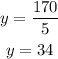
Now, we can substitute this values in order to find the measure of each angle:
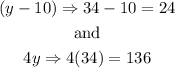
Therefore, the angles are 24, 136 and 20 degrees.