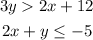
To graph a system of inequalities you need to find the coordinates of 2 points on each inequality (as they are lineal inequalities):
-----------------------
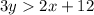
Solve for y: divide both sides of the inequality into 3:
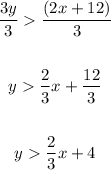
Find the points as in a equation:
If x is 0:
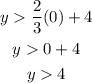
First point (0 , 4)
If x is 6
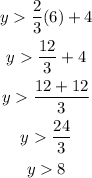
Second point ( 6, 8 )
As the inequality is y greather than (2/3x+4) you draw a dot line that go through the two points and shade the area over the line:
--------------------------
Repeat the process to find two points in the second inequality:
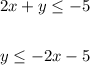
If x is 0:
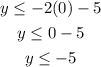
First point (0 , -5)
If x is -5

Second point ( -5 , 5)
As the inequality is y less than or equal to (-2x-5) you draw a line that go through the two points and shade the area under that line:
------------------
Then, you get the next graph for the system of inequalities:
The solution is the area shaded by both inequalities.