First question.
The probability of any event is given by:
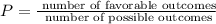
In this study we have a total of 87 people with hypertension and 180 people was studied, then we have:
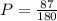
Therefore, the probability of selecting an individual with hypertension is 87/180
Second question.
The conditional probability of event B given that event A already happened is given by:
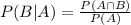
For this question let B be the event "The person is experiencing hypertension" and let event A be "The person is a heavy smoker". From the table we notice that a total of 49 individuals are heavy smokers and that 30 individuals are both heavy smokers and experiencing hypertension. Then we have:
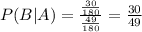
Therefore, the probability is 30/49
Third questions.
We know that two events are independent if and only if:
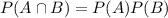
Using the events as we did in the previous question we have:
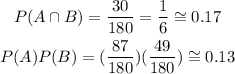
Clearly the condition is not hold. Which means that the events are dependent