Question

Find the length of the radius Round to the nearest whole number

Answer 1

Step-by-step explanation

Let's picture the situation described by the exercise:

We have a circle with radius r, and a (green) sector with an area of 361.6 m^2, and with a central angle of 288 degrees. To solve this exercise, we merely need to remember the formula for the area (AS) of a sector:

`AS=\frac{\text{angle}}{360}\cdot\pi\cdot r^2.`

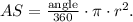
For we are looking for the radius, we need to solve this "equation" for the variable r:

`\begin{gathered} AS=\frac{\text{angle}}{360}\cdot\pi\cdot r^2, \\ 360\cdot AS=(\text{angle)}\cdot\pi\cdot r^2, \\ \frac{360\cdot AS}{(\text{angle)}\cdot\pi}=r^2, \\ r^2=\frac{360\cdot AS}{(\text{angle)}\cdot\pi}, \\ r=\sqrt[]{\frac{360\cdot AS}{(\text{angle)}\cdot\pi}}\text{.} \end{gathered}`

Evaluating for the values of AS and "angle" of our sector, we get

`\begin{gathered} r=\sqrt[]{\frac{360\cdot AS}{(\text{angle)}\cdot\pi}}\leftarrow\begin{cases}AS=361.6m^2 \\ angle=288 \\ \pi=3.14\end{cases}, \\ r=\sqrt[]{(360\cdot361.6m^2)/(288\cdot(3.14))}, \\ r\approx\sqrt[]{143.9m^2}, \\ r\approx11.9m. \end{gathered}`

Finally, we must round up the value of r we just obtained. Note that the first decimal place (9) of 11.9 is greater than 5, then by the rounding rule we must add one tenth, to get

`r=12m`

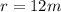
Answer

The radius of the circle is

`r=12m`