Question

Here is my problem. Hopefully you will be able to help me!

Answer 1

All the items use the same form of exponential equation:

`f(t)=ab^t`

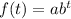
In this form, the initial value is always "a", because for t = 0:

`f(0)=ab^0=a`

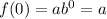
And whether it is a exponential growth of decay we can see by the "b" value.

It is an exponential growth if:

`b>1`

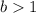
And it is an exponential decay if:

`0Now, for the alternatives.<p>a)</p>[tex]\begin{gathered} a=2 \\ b=(2)/(5) \end{gathered}`

So the initial value is 2 and "b" is less than 1, so it is an exponential decay.

b)

`\begin{gathered} a=2 \\ b=(5)/(3) \end{gathered}`

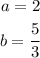
So the initial value is 2 and "b" is greater than 1, so it is an exponential growth.

c)

`\begin{gathered} a=(2)/(3) \\ b=3 \end{gathered}`

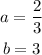
So the initial value is 2/3 and "b" is greater than 1, so it is an exponential growth.

d)

`\begin{gathered} a=(2)/(3) \\ b=(1)/(3) \end{gathered}`

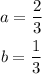
So the initial value is 2/3 and "b" is less than 1, so it is an exponential decay.

e)

`\begin{gathered} a=(3)/(2) \\ b=(2)/(3) \end{gathered}`

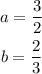
So the initial value is 3/2 and "b" is less than 1, so it is an exponential decay.